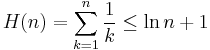Set cover problem
The set covering problem (SCP) is a classical question in computer science and complexity theory. It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms.[1] It was also one of Karp's 21 NP-complete problems shown to be NP-complete in 1972.
Given a set of elements 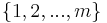 (called the universe) and
(called the universe) and  sets whose union comprises the universe, the set cover problem is to identify the smallest number of sets whose union still contains all elements in the universe. For example, assume we are given the following elements
sets whose union comprises the universe, the set cover problem is to identify the smallest number of sets whose union still contains all elements in the universe. For example, assume we are given the following elements 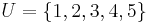 and sets
and sets 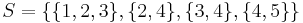 . Clearly the union of all the sets in
. Clearly the union of all the sets in  contain all elements in
contain all elements in  . However, we can cover all of the elements with the following, smaller number of sets:
. However, we can cover all of the elements with the following, smaller number of sets: 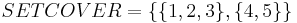 .
.
More formally, given a universe 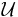 and a family
and a family 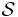 of subsets of
of subsets of 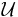 , a cover is a subfamily
, a cover is a subfamily 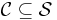 of sets whose union is
of sets whose union is 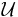 . In the set covering decision problem, the input is a pair
. In the set covering decision problem, the input is a pair 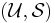 and an integer
and an integer  ; the question is whether there is a set covering of size
; the question is whether there is a set covering of size  or less. In the set covering optimization problem, the input is a pair
or less. In the set covering optimization problem, the input is a pair 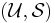 , and the task is to find a set covering that uses the fewest sets.
, and the task is to find a set covering that uses the fewest sets.
The decision version of set covering is NP-complete, and the optimization version of set cover is NP-hard.
| Covering-packing dualities | |
| Covering problems | Packing problems |
|---|---|
| Minimum set cover | Maximum set packing |
| Minimum vertex cover | Maximum matching |
| Minimum edge cover | Maximum independent set |
Contents[hide] |
Integer linear program formulation
The minimum set cover problem can be formulated as the following integer linear program.[2]
| minimize | 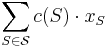 |
(minimize the total cost) | |
| subject to | 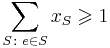 |
for all 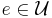 |
(cover every element of the universe) |
 |
for all 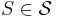 . . |
(every set is either in the set cover or not) |
This ILP belongs to the more general class of ILPs for covering problems. The integrality gap of this ILP is at most 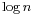 , so its relaxation gives a factor-
, so its relaxation gives a factor-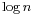 approximation algorithm for the minimum set cover problem (where
approximation algorithm for the minimum set cover problem (where 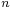 is the size of the universe).[3]
is the size of the universe).[3]
Hitting set formulation
Set covering is equivalent to the Hitting set problem. It is easy to see this by observing that an instance of set covering can be viewed as an arbitrary bipartite graph, with sets represented by vertices on the left, the universe represented by vertices on the right, and edges representing the inclusion of elements in sets. The task is then to find a minimum cardinality subset of left-vertices which covers all of the right-vertices. In the Hitting set problem, the objective is to cover the left-vertices using a minimum subset of the right vertices. Converting from one problem to the other is therefore achieved by interchanging the two sets of vertices.
Greedy algorithm
The greedy algorithm for set covering chooses sets according to one rule: at each stage, choose the set that contains the largest number of uncovered elements. It can be shown[4] that this algorithm achieves an approximation ratio of 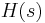 , where
, where  is the size of the largest set and
is the size of the largest set and 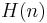 is the
is the  -th harmonic number:
-th harmonic number:
There is a standard example on which the greedy algorithm achieves an approximation ratio of 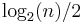 . The universe consists of
. The universe consists of 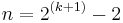 elements. The set system consists of
elements. The set system consists of  pairwise disjoint sets
pairwise disjoint sets  with sizes
with sizes 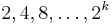 respectively, as well as two additional disjoint sets
respectively, as well as two additional disjoint sets 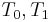 , each of which contains half of the elements from each
, each of which contains half of the elements from each 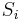 . On this input, the greedy algorithm takes the sets
. On this input, the greedy algorithm takes the sets  , in that order, while the optimal solution consists only of
, in that order, while the optimal solution consists only of 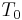 and
and 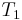 . An example of such an input for
. An example of such an input for 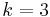 is pictured on the right.
is pictured on the right.
Inapproximability results show that the greedy algorithm is essentially the best-possible polynomial time approximation algorithm for set cover (see Inapproximability results below), under plausible complexity assumptions.
Low-frequency systems
If each element occurs in at most f sets, then a solution can be found in polynomial time that approximates the optimum to within a factor of f as follows: while an uncovered element exists, add all (at most f) sets which contain this element to the cover. In the end we end up with some cover, which we output. To see that this is an f-approximation it suffices to note that every time we add f sets, at least one of those is in an optimal cover as well. For f = 2, this is the normal approximation algorithm for vertex cover.
See k-approximation of k-hitting set for an f-approximation of weighted set cover.
Inapproximability results
Lund & Yannakakis (1994) showed that set covering cannot be approximated in polynomial time to within a factor of 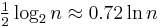 , unless NP has quasi-polynomial time algorithms. Feige (1998) improved this lower bound to
, unless NP has quasi-polynomial time algorithms. Feige (1998) improved this lower bound to 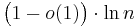 under the same assumptions, which essentially matches the approximation ratio achieved by the greedy algorithm. Raz & Safra (1997) established a lower bound of
under the same assumptions, which essentially matches the approximation ratio achieved by the greedy algorithm. Raz & Safra (1997) established a lower bound of 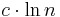 , where
, where  is a constant, under the weaker assumption that P
is a constant, under the weaker assumption that P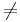 NP. A similar result with a higher value of
NP. A similar result with a higher value of  was recently proved by Alon, Moshkovitz & Safra (2006).
was recently proved by Alon, Moshkovitz & Safra (2006).
Related problems
- Hitting set is an equivalent reformulation of Set Cover.
- Vertex cover is a special case of Hitting Set.
- Edge cover is a special case of Set Cover.
- Set packing is the dual problem of Set Cover.
- Maximum coverage problem is to choose at most k sets to cover as many elements as possible.
- Dominating set is the problem of selecting a set of vertices (the dominating set) in a graph such that all other vertices are adjacent to at least one vertex in the dominating set. The Dominating set problem was shown NP complete by reducing Set cover to it.
Notes
- ^ Vazirani (2001, p. 15)
- ^ Vazirani (2001, p. 108)
- ^ Vazirani (2001, pp. 110–112)
- ^ Chvatal, V. A Greedy Heuristic for the Set-Covering Problem. Mathematics of Operations Research Vol. 4, No. 3 (Aug., 1979), pp. 233-235
References
- Alon, Noga; Moshkovitz, Dana; Safra, Shmuel (2006), "Algorithmic construction of sets for k-restrictions", ACM Trans. Algorithms (ACM) 2 (2): 153–177, doi:10.1145/1150334.1150336, ISSN 1549-6325.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), Introduction to Algorithms, Cambridge, Mass.: MIT Press and McGraw-Hill, pp. 1033–1038, ISBN 0-262-03293-7
- Feige, Uriel (1998), "A threshold of ln n for approximating set cover", Journal of the ACM (ACM) 45 (4): 634–652, doi:10.1145/285055.285059, ISSN 0004-5411.
- Lund, Carsten; Yannakakis, Mihalis (1994), "On the hardness of approximating minimization problems", Journal of the ACM (ACM) 41 (5): 960–981, doi:10.1145/185675.306789, ISSN 0004-5411.
- Raz, Ran; Safra, Shmuel (1997), "A sub-constant error-probability low-degree test, and a sub-constant error-probability PCP characterization of NP", STOC '97: Proceedings of the twenty-ninth annual ACM symposium on Theory of computing, ACM, pp. 475–484, ISBN 978-0-89791-888-6.
- Vazirani, Vijay V. (2001), Approximation Algorithms, Springer-Verlag, ISBN 3-540-65367-8